

Podem prendre l'exemple de la conca rectangular com una versió en miniatura d'una conca oceànica als subtròpics a l'hemisferi nord (sense força de Coriolis). Les línies de corrent que vèiem eren trajectòries de l'aigua movent-se en un gir subtropical en moviment estacionari.
Suposem que el gir no està en estat estacionari sinó que s'accelera i es frena en resposta a variacions estacionals de la força del vent. El corrent, i com a conseqüència la funció de corren, són llavors funcions del temps.
Suposem un augment i decreixement periòdic al voltant d'un valor mig (que pot representar una intensificació del gir durant l'hiver quan els vents són més forts i un afebliment durant l'estiu quan els vents són lleugers).
Suposem les mateixes components de la velocitat com abans però les farem dependent del temps:
\[ \begin{matrix} u = -U_0 \sin \big(\dfrac{\pi x}{L} \big) \cos \big(\dfrac{\pi y}{B} \big) \big( 1 + 0.5 \sin \big(2 \dfrac{\pi t}{T} \big) \big), & \text{component est} \\ \\ v = V_0 \sin \big(\dfrac{\pi x}{L} \big) \cos \big(\dfrac{\pi y}{B} \big) \big( 1 + 0.5 \sin \big(2 \dfrac{\pi t}{T} \big) \big), & \text{component nord} \\ \\ \text{amb}\;\; U_0 = V_0 L/B, \quad t = \text{temps}, \quad T = \text{període} & \end{matrix}\]
Amb les components de la velocitats dependent del temps ψ esdevé
\[ \psi = \dfrac{U_0 B}{\pi} \sin \big(\dfrac{\pi x}{L} \big) \sin \big(\dfrac{\pi y}{B} \big) \;\big( 1 + 0.5 \sin \big(2 \dfrac{\pi t}{T} \big) \big) + \text{constant d'integració}. \]
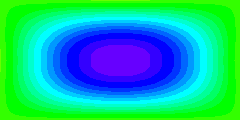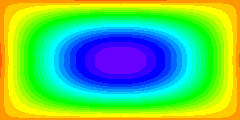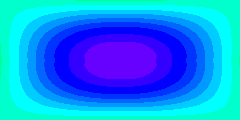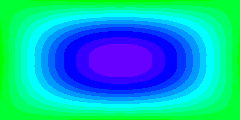
Les línies de corrent estan definides com a línies de valor constant de la funció de corrent. Si la funció de corrent varia amb el temps, les posicions de les línies de corrent varien amb el temps. L'animació mostra això ensenyant els valors de la funció de corrent amb patrons de color. L'inici del temps de la seqüència correspon a la situació promig, que és idèntica al camp de la funció de corrent de l'estat estacionari que hem vist a la pàgina precedent.
Òbviament, el moviment de l'aigua no segueix el moviment pulsant de les línies de corrent. Les parcel·les d'aigua encara seguiran els mateixos camins que en estat estacionari però es mouran més ràpidament durant una part del cicle i més lentament durant l'altra part.
Resumint, la demostració de les línies de corrent com a indicadors lagrangians del moviment de l'aigua ens ensenya que
Les línies de corrent són trajectòries només sota condicions de flux estacionari.
Una descripció lagrangiana dels corrents oceànics es pot fer només col·locant un objecte derivant a l'oceà i dibuixant la seva posició amb el temps. Aquest no és un dibuix vectorial en el sentit estricte, ja que les posicions estan donades per un senzill parell de coordenades x i y, i no per un mòdul i una direcció (el mòdul i la direcció del corrent estan només determinats per una seqüència de posicions). El dibuix de les posicions no es discutirà en aquest exercici.