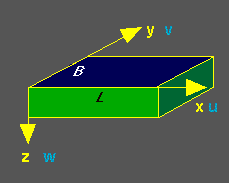
Considerem una conca rectangular de fondària uniforme amb una amplada B, longitud L i plena d'aigua. L'aigua es mou estacionariament amb moviment contra les agulles del rellotge, és a dir que no s'accelera ni es frena.
Per conveniència assumim que l'eix allargat de la conca (la longitud L) apunta cap a l'est i l'eix curt (l'amplada B) cap al nord.
Assumim a més a més que no hi ha moviment vertical, que vol dir que el moviment de l'aigua està completament descrit per només dues components, la component zonal u i la component meridional v. En altres paraules és bi-dimensional:
\[ \begin{matrix} \text{component est} & \text{component nord} \\ u = -U_0 \sin \big(\dfrac{\pi x}{L} \big) \cos \big(\dfrac{\pi y}{B} \big), & v = V_0 \sin \big(\dfrac{\pi x}{L} \big) \cos \big(\dfrac{\pi y}{B} \big) \\ \text{amb}\;\;U_0 = V_0\; L/B & \end{matrix} \]
El model de conca fa servir els valors L = 40 km, B = 20 km, V0 = 0.1 ms-1 (que dona U0 = 0.2 m s-1).
La velocitat així definida és bi-dimensional, que vol dir que la velocitat vertical w és idènticament zero. Això es pot verificar amb l'equació de continuïtat,
\[ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} = 0 \]
Les components de la velocitat donades satisfan l'equació de la forma
\[ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} = 0 \]
Si el moviment de l'aigua és bi-dimensional, és possible definir la funció de corrent. La funció de corrent ψ es defineix a través de les equacions
\[ - \dfrac{\partial \psi}{\partial y} = u, \quad\quad \dfrac{\partial \psi}{\partial x} = v \]
Amb les components de la velocitat donades, ψ esdevé
\[ \psi = \dfrac{U_0 B}{\pi} \sin \big(\dfrac{\pi x}{L} \big) \sin \big(\dfrac{\pi y}{B} \big) + \text{constant d'integració}. \]
Les funcions de corrent són contorns al llarg dels quals ψ és constant (la funció de corrent manté el mateix valor). Per a un valor constant donat ψ = ψ0, les coordenades x, y dels punts de la funció de corrent venen donades per la relació entre x i y
\[ \sin \big(\dfrac{\pi x}{L} \big) \sin \big(\dfrac{\pi y}{B} \big) \]
on la constant vé donada per
\[ \dfrac{\pi}{ U_0 B} \psi_0 \]
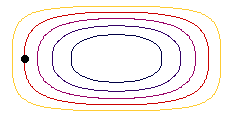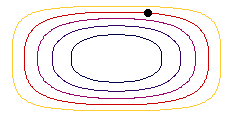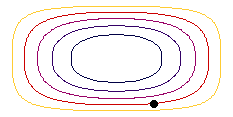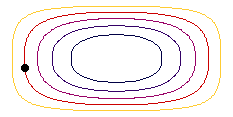
En cas de moviment estacionari, les línees de corrent indiquen les formes en que les partícules es mouen. L'animació mostra les línies de corrent com exemple de la conca rectangular en diferents colors i una parcel·la d'aigua (punt negre) en moviment en estat estacionari.
Els contorns que indiquen les formes en que les partícules es mouen s'anomenen trajectòries. Trobar les trajectòries per a un camp de flux donat és una aproximació Lagrangiana a l'estudi dels corrents.
Podem fer un sumari de tot això dient que
Sota condicions de flux estacionari, les línies de corrent són trajectòries.
