The last lecture foreshadowed the development of place-value number systems as one of the greatest achievements of the human mind. We all use a place-value number system every day without realizing what a magnificent invention it is. The principle appears so simple that it is hard to believe how long it took before a human mind came up with the idea.
To see the giant leap forward let us try a simple calculation: How do you multiply 212 by 16? In Roman numerals this is written as CCXII * XVI. Multiplication of CCXII with XVI is obviously not straightforward. In a position-value system the operation follows very simple rules. All we need to know is the basic multiplication table and the rules for addition:
212 x 16
32
16
32
3392
place-value number systems were developed independently in
We see from the list that the Babylonian place-value number system preceded all others by nearly two thousand years. Why did it not survive? Why did quite advanced civilizations struggle on with absolute value systems until at least 200 BC, if not later, when the idea had already been around a millennium earlier?
Babylon became the capital of southern Mesopotamia in about 1780 BC. It developed into the biggest city of the world of its time, and its temples and public buildings reached world fame. (The Bible mentions Babylon's 91 m tall ziggurat (temple pyramid) as the "Tower of Babel", built to defy the gods through its height.)
The Babylonian scientists adopted the Sumerian cuneiform script for their numbers but changed the way of writing them down drastically. Instead of building a number by adding as many basic number elements as necessary they began to build them by adding powers of the number base. Here are two examples of Sumerian and Babylonian number notation. The first row gives the base units, the second row the example how the number 1859 is constructed, the third row the example of the number 4818:
| Sumerian system | Babylonian system | |
| base units | 1, 10, 60, 600, 3600, 36000 | 1, 60, 602, 603, 604 |
| 1859 | 600 + 600 + 600 + 50 + 9 | 30 (x 60) + 59 (x 1) |
| 4818 | 3600 + 600 + 600 + 18 | 1 (x 602) + 20 (x 60) + 18 (x 1) |
The new notation was a true revolution. It used the same principle that we use today when we write our numbers in decimal notation:
| 1859 | 1 (x 103) + 8 (x 102) + 5 (x 10) + 9 (x 1) |
| 4818 | 4 (x 103) + 8 (x 102) + 1 (x 10) + 8 (x 1) |
Babylonian scientists could therefore use the same simple rules for multiplication and long division that we use some 4,000 years later. The admiration of the place-value number system expressed by the French mathematician Pierre-Simon Laplace in the early 19th century is an acknowledgment of the genius exhibited by some unknown scientist-priests of Babylon: "The idea is so simple that this very simplicity is the reason for our not being sufficiently aware how much admiration it deserves."
There is no doubt that science in Babylon made rapid progress after the invention of the place-value number system. But there was still a long way to go. To begin with, our modern notation indicates every digit in a number through a single symbol (one from the set of numerals 0 - 9). The Babylonian system still required several symbols to indicate the value of each power of the base 60 in a number. Correct spacing of the pictographs in a Babylonian number was therefore of utmost importance.
To demonstrate the problem, imagine a number that uses four places, with the corresponding allocations "1 25 12 2". If this number is copied without accurate attention to the spaces it can appear as "1 2 5 12 2" or as "1 25 1 22" - obviously many mistakes are possible. The Babylonian notation is often not very specific, and calculation errors must have been a regular occurrence.
The much bigger problem, however, was the lack of a pictograph for "zero". As strange as it may seem, the Babylonian scientists not only had no sign for zero, they had no concept of zero. This is evident from Babylonian mathematical textbooks which contain equations in their example calculations such as
"20 - 20 = well, you know ...
20 - 5 - 5 - 5 - 5 = We are running out of grains." -
Every equation with a zero result receives an evasive answer, with the occasional allusion at the old system of counting by association with pebbles or grains.
We are today so accustomed to using a place-value number system with a zero that it appears difficult to imagine how people could have lived without the concept of "nothing". Before we come to the rash conclusion that our contemporaries - and maybe we with them - are smarter than the people of ancient Babylon, let us remind ourselves that people only develop new scientific concepts and tools when they need them for their daily lives.
Absolute number systems have no need for a zero: In Roman notation the number 1006 is written as MVI. Commerce and business also get along well without a zero. If someone takes out a loan, the amount of the loan is stamped into a clay tablet; the tablet is destroyed when the loan is repaid. At no point in the transaction does the need arise to write out a document "A repaid the loan to B and now owes B zero sheep." The need for a zero only arises with the introduction of a place-value number system.
The Babylonians left a space for a zero, a procedure open to much interpretation. Does a space signify one zero or two? What if there is a zero at the end of the number, how can you make space visible at the end?
For 1400 years the Babylonian scientists did extensive and complicated astronomical calculations without a symbol for zero. In about 400 BC they introduced the script character for "space" to indicate a zero. At that time everyone else had already switched to the much more convenient decimal system of Egypt, and the use of the Babylonian place-value number system remained restricted to astronomy. Eventually it fell into disuse as Babylon was eclipsed by Alexandria, which was founded in 332 BC.
The use of one number system for daily life and a different one for science is not as unusual as it may sound. Examples can be seen even today. People in the United States of America still use feet and inches for length (1 foot = 12 inches) and gallons, quarts and pints for volumes (1 gallon = 4 quarts = 8 pints), while scientists in the USA use the metric system that is used everywhere else in the world.
At about the time when the Babylonian number system was forgotten in the Middle East, a new and superior place-value number system was developed in China. It avoided the first of the Babylonian problems (the question of correct spacing) but shared its second problem: It did not include a zero.
China had (and still has) several ways of writing numbers. There are characters for calligraphy, for daily use and for other applications. One of the various character systems for numbers, developed between 200 BC and 200 AD, is a true position-value system. It uses the base 10 and the auxiliary base 5 and represents the numerals 1 - 9 as pictographs of bamboo sticks:
Bamboo sticks were the calculation tool in China; they were used on a board with regular squares, much like a board for a chess game but without the alternating colours.
The problem of correct spacing did of course not occur on a calculation or checker board, where every digit of each number has its allocated square. To avoid misunderstandings when numbers were written in text scrolls the Chinese scientists had a second version for the numerals 1 - 9:
Both versions could be used in any position. However, if odd positions use the first version, even positions have to use the second version, and vice versa. This system neatly separates each position and allowed very compact writing of numbers.
The Chinese numerals were copies of bamboo sticks used on calculation boards. Because a calculation board used empty squares for zero, the Chinese number system had no numeral for zero. This situation continued for some 600 - 1000 years after the original invention of the place-value number system in China.
Some time after 800 AD travelling scholars imported the idea of a special symbol for zero from India, and the Chinese scientists added the Indian symbol "0" to their own set of numerals. This created the conditions for great advances in Chinese mathematics and science. Systems of linear equations had been solved on the calculation board well before 200 AD, and methods for solving them and ways to find solutions to polynomial equations were explained in textbooks. The sequence of binomial coefficients (known in the European civilization as "Pascal's triangle") was published in China in 1303 AD. European science discovered the binomial coefficients again 400 years later, when Isaac Newton postulated its structure and Daniel Bernoulli found the mathematical proof in 1716.
While Chinese and Indian mathematics progressed rapidly in Asia, the Maya civilization of Central America developed a place-value number system of its own that included a zero. Invented around 500 AD, it used the main base 20 and the auxiliary base 5. The numerals were pictographs of pebbles and sticks. The combination of the base 20 and auxiliary base 5 with two easily recognizable simple geometrical forms made the Maya numbers very easy to read:
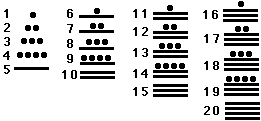
Why did the Maya include a zero in their number system? It is probably impossible to find an unequivocal answer to that question today. The Maya civilization kept an excellent record of its day to day activities and major events; but the Christian missionaries who accompanied the Spanish conquerors in the 16th century could not read Maya script and burnt nearly all Maya records as "pagan superstition".
Most of our information on Maya mathematics comes from buildings and sculptures. The Maya civilisation documented all regular major events by erecting monuments. These monuments were richly decorated and meticulously organised into regular squares that indicated the date of the recorded event. No square was allowed to remain empty. It appears that this aesthetic-religious requirement brought about the early introduction of the zero: If an event happened on a day that required a zero in one digit of the date, the corresponding square on the monument was filled with the zero sign.
The few written documents that survived the Spanish book burnings testify for the high development of Maya astronomy and mathematics. The Maya number system was actually somewhat more complicated than described here because it was tuned specifically to calendar applications. Lecture 7, which deals with calendars of the world, will therefore return to Maya numbers in more detail.
Ifrah, G. (2000) Universal History of Numbers. John Wiley & Sons. Translated from Ifrah, G. (1981) Histoire Universelle des Chiffres, (Seghers).
| next lecture |