

This utility calculates and plots the amplitude and phase of a co-oscillation tide in a narrow gulf. The solution is found for one tidal constituent at a time. It is advisable to read the theory, model and example before proceeding to an application.
Projects for which this utility can be used:
This utility is based on A. K. Easton (1978) A reappraisal of the tides in Spencer Gulf, South Australia. Australian Journal of Marine and Freshwater Research 29, 467 - 477.
Theoretical background to the utility to calculate and plot the amplitude and phase of a co-oscillation tide in a narrow gulf.
The analysis starts from the linearised Equations of Motion for a frictionless ocean:
\begin{eqnarray*} \dfrac{\partial u}{\partial t} - f v + \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} & = & 0 \\ \dfrac{\partial v}{\partial t} + f u + \dfrac{1}{\rho} \dfrac{\partial p}{\partial y} & = & 0 \\ - g \rho + \dfrac{\partial p}{\partial z} & = & 0 \end{eqnarray*}
The third equation is also known as the hydrostatic equation.
If the equations are applied to a narrow basin or gulf, movement can only occur in two dimensions and the Coriolis force can be neglected. Taking the axis of the gulf in the x-direction we then have:
\begin{eqnarray*} \dfrac{\partial u}{\partial t} + \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} & = & 0 \\ - g \rho + \dfrac{\partial p}{\partial z} & = & 0 \end{eqnarray*}
The stratification can be ignored in the investigation of surface tides, so density $\rho$ can be replaced by a constant reference density $\rho_0$, and the hydrostatic equation can be integrated to give pressure p as
\[ \mathbf{p = g (H + \zeta)} \]
where $\mathbf{H}$ is the depth and $\mathbf{\zeta (x)}$ the surface elevation, or the shape of the sea surface along the basin. This expression for $\mathbf{p}$ can be introduced into the Equation of motion. For a basin of uniform (constant) depth this leads to
\[ \dfrac{\partial u}{\partial t} + g \dfrac{\partial \zeta}{\partial x} = 0 \]
When this result is multiplied with the (constant) width $\mathbf{B}$ of the basin the result is
\[ \dfrac{\partial q}{\partial t} + g \;S \;\dfrac{\partial \zeta}{\partial x} = 0 \]
Where $\mathbf{S = B \cdot H}$ is the cross-sectional area and $\mathbf{q = u \cdot B}$ is the transport through the cross-sectional area.
We now have an equation for the unknown target variable $\mathbf{\zeta (x)}$ and the unknown transport $\mathbf{q(x)}$, which we have to eliminate. This is done with the help of the continuity equation, which for an ocean of constant density is
\[ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} = 0 \]
When vertically integrated and multiplied by the width of the basin this equation becomes
\[ \dfrac{\partial q}{\partial x} + B \;\dfrac{\partial \zeta}{\partial t} = 0 \]
The numerical scheme for the utility to calculate and plot the amplitude and phase of a co-oscillation tide in a narrow gulf.
The model is based on the linearised vertically integrated Equations of Motion and the continuity equation in the form derived in the theory page:
\begin{eqnarray*} \dfrac{\partial q}{\partial t} + g S \dfrac{\partial \zeta}{\partial x} & = & 0 \\ \dfrac{\partial q}{\partial x} + B \dfrac{\partial \zeta}{\partial t} & = & 0 \end{eqnarray*}
A co-oscillation tide is a standing wave generated by tidal movement at the open end of the basin or gulf. The two unknowns $\zeta (x)$> and $q$ can therefore be written as
\begin{eqnarray*} \zeta (x, t) & = Z(x) e^{i \omega t} \\ q (x, t) & = Q(x) e^{i \omega t} \end{eqnarray*}
where $\mathbf{omega}$ is the frequency of a tidal constituent. Introducing these forms for the unknowns into the equations gives a set of coupled equations for $\mathbf{Z}$ and $\mathbf{Q}$:
\begin{eqnarray*} i \omega Q + g S Z(x) \dfrac{\partial Z}{\partial x} & = 0 \\ \dfrac{\partial Q}{\partial x} + i \omega B Z & = 0 \end{eqnarray*}
These equations can be solved numerically if the width $\mathbf{B}$ and the cross-sectional area $\mathbf{S}$ vary only slowly in $x$. The gulf or basin is divided into sections of length $\mathbf{\Delta x}$, and the equations are written in finite difference form:
\begin{eqnarray*} Q_{k+1} & = & Q_{k-1} - 2 i \omega B \Delta x Z_k \\ Z_{k+2} & = & Z_k - 2 \dfrac{2 i \omega \Delta x}{g S_{k+1}} Q_{k+1} \end{eqnarray*}
The computation begins at the head of the gulf with $Q_0 = 0$ and $Z_1 = 1$, and $Q$ and $Z$ are evaluated at alternate sections.
The effect of bottom friction on the tidal wave can be incorporated through a linear damping term. If friction is assumed to be proportional to the bottom velocity, which is proportional to the transport $\mathbf{q}$, the vertically integrated equations become
\begin{eqnarray*} \dfrac{\partial q}{\partial t} + g S \dfrac{\partial \zeta}{\partial x} + r q = & 0 \\ \dfrac{\partial q}{\partial x} + B \dfrac{\partial \zeta}{\partial t} = & 0 \end{eqnarray*}
where $\mathbf{r}$ is a friction parameter; $1/\mathbf{r}$ corresponds to the time over which the tidal amplitude would decrease to $1/e$ of its original value if the tidal forcing would be switched off. The finite difference equations are then
\begin{eqnarray*} Q_{k+1} & = & Q_{k-1} - 2 i \omega B \Delta x Z_k \\ Z_{k+2} & = & Z_k - \dfrac{2 (i \omega + r) \Delta x}{g S_{k+1}} Q_{k+1} \end{eqnarray*}
Spencer Gulf is one of two gulfs that extend northward from the south Australian coast (Figure 1). Tides along the south coast of Australia are relatively moderate in size, with amplitudes of the four major constituents of 0.15 - 0.30 m. Tides in the gulfs are generally larger and increase towards the heads. The following table gives tidal constants for ports around Spencer Gulf and some other locations.
| port | M2 | S2 | K1 | O1 | 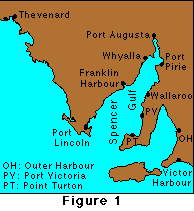 |
||||
| H (m) | phase (º) | H (m) | phase (º) | H (m) | phase (º) | H (m) | phase (º) | ||
| Spencer Gulf | |||||||||
| Port Augusta | 0.68 | 212 | 0.74 | 273 | 0.45 | 82 | 0.29 | 54 | |
| Port Pirie | 0.49 | 200 | 0.54 | 263 | 0.41 | 80 | 0.28 | 52 | |
| Whyalla | 0.42 | 185 | 0.45 | 245 | 0.40 | 73 | 0.26 | 45 | |
| Wallaroo | 0.17 | 130 | 0.17 | 187 | 0.32 | 62 | 0.22 | 34 | |
| Franklin Harbour | 0.22 | 114 | 0.23 | 173 | 0.30 | 61 | 0.20 | 24 | |
| Port Victoria | 0.18 | 70 | 0.18 | 127 | 0.23 | 52 | 0.20 | 24 | |
| Point Turton | 0.18 | 67 | 0.21 | 117 | 0.26 | 53 | 0.17 | 22 | |
| Port Lincoln | 0.23 | 35 | 0.26 | 87 | 0.23 | 29 | 0.16 | 2 | |
| Other ports | |||||||||
| Outer Harbour | 0.50 | 105 | 0.49 | 176 | 0.25 | 50 | 0.16 | 24 | |
| Thevenard | 0.30 | 1 | 0.37 | 47 | 0.19 | 24 | 0.13 | 359 | |
| Victor Harbour | 0.14 | 343 | 0.14 | 46 | 0.18 | 30 | 0.14 | 356 | |
The table shows that the amplitudes of the M2 and S2 constituents have a minimum in the centre of the gulf near Wallaroo and that the phases of these constituents change from the mouth of the Gulf at Port Lincoln to the head at Port Augusta by 180º; in other words, these two constituents co-oscillate with the tides of the Southern Ocean as a second order seiche. In contrast, the amplitudes of the K1 and O1 constituents increase monotonically from the mouth to the head, and their phases are nearly constant along the gulf, indicating that these constituents form a first order seiche.
|
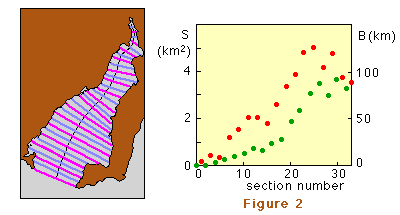
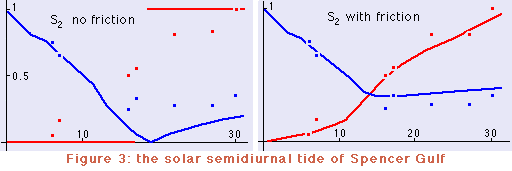
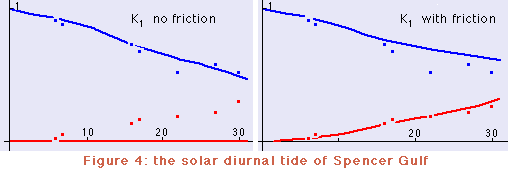
Figure 2 shows the division of the gulf into 33 compartments of 10 km length (the Δx of the finite difference model) and the associated width B (red dots) and cross-sectional area S (green dots). Values for B have to be provided for odd locations (magenta lines), values for S for even locations (dark grey lines). Figure 3 compares the result of the model for the S2 constituent with the observed amplitudes and phases. The amplitude, normalised to unity at the head of the gulf, is shown in blue; the phase, normalised to (ie divided by) 180º, is shown in red. Observations are shown by squares. (Note that without friction the phase can only be equal to 0º or 180º.) Figure 4 gives the same comparison for the K1 constituent. |
 |
A numerical model of the co-oscillation tide in Spencer Gulf, South Australia, or of any other semi-enclosed narrow basin.
The application of the numerical model is available in two versions. Both perform the same calculations, but the result is displayed in tabular form in version 1 and in graphical form in version 2.
Both versions return a magnification factor, which indicates how close you are to resonance. The factor is calculated as the ratio of the amplitude at the head over the amplitude at the mouth. (Remember that the amplitude at the head is normalised to 1 and the calculations proceed towards the mouth, so resonance does not result in huge amplitudes but produces a very large magnification factor.)
For the Spencer Gulf situation both versions also return two rms errors (one for amplitude and one for phase) for the S2 and K1 constituents. They compare the model with observed values at tide gauge locations.
Select the version you want to use:
|
|
|
basin data are Component: tide results are |
Magnification: RMS errors: amplitude phase |