Aquesta secció permet calcular i dibuixar l'amplitud i la fase d'una co-oscil·lació de marea en un golf estret. La solució es troba numèricament per cada component de marea separadament. Es recomana llegir la teoria, el model i l'exemple abans de procedir amb l'aplicació.
Aspectes pels quals aquesta aplicació es pot fer servir:
Aquesta secció està basada en el treball de A. K. Easton (1978), A reappraisal of the tides in Spencer Gulf, South Australia. Australian Journal of Marine and Freshwater Research 29, 467-477.
L'anàlisi comença a partir de les Equacions del Moviment linearitzades per un oceà sense fricció:
\begin{eqnarray*} \dfrac{\partial u}{\partial t} - f v + \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} & = & 0 \quad (1)\\ \dfrac{\partial v}{\partial t} + f u + \dfrac{1}{\rho} \dfrac{\partial p}{\partial y} & = & 0 \quad (2)\\ - g \rho + \dfrac{\partial p}{\partial z} & = & 0 \quad (3) \end{eqnarray*}
(1) i (2) són les equacions lineals del balanç de moment de les components horitzontals. La darrera equació (3) és coneguda com l'equació del balaç hidrostàtic, que expressa el balanc entre la força gravitatòria i el gradient vertical de pressions.
Si les equacions s'apliquen a una badia o conca estreta, es pot condiderar que el moviment és en dues dimensions i la força de Coriolis es pot menysprear. Considerant l'eix del golf segons la direcció $x$, llavors tenim:
\begin{eqnarray} \dfrac{\partial u}{\partial t} + \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} & = & 0 \quad (4)\\ - g \rho + \dfrac{\partial p}{\partial z} & = & 0 \label{eq} \end{eqnarray}
L'estratificació pot ignorar-se en la recerca de marees de superfície, de forma que la densitat $\rho$ pot reemplaçar-se per una densitat constant de referència $\rho_0$, i llavors l'equació hidrostàtica pot integrar-se per a trobar la pressió $p$ com
\[ p = \rho_0 g (H + \mathbf{\zeta}) \]
on $H$ és la fondària i $\mathbf{\zeta} (x)$ correspon a l'elevació de la superfície del mar al llarg de la badia. Ara $\mathbf{p}$ pot ser introduïda en (4), i suposant una badia de fondària uniforme ($H \approx $ constant) això implica
\[ \dfrac{\partial u}{\partial t} + g \dfrac{\partial \zeta}{\partial x} = 0 \]
Si ara multipliquem per l'amplada (constant) $\mathbf{B}$ i la fondària de la conca $\mathbf{H}$ el resultat és
$$\bbox[10px, border:2px solid red] { \dfrac{\partial q}{\partial t} + g \;S \;\dfrac{\partial \zeta}{\partial x} = 0, \quad (5)} $$
on $\mathbf{S = B \cdot H}$ és l'àrea de la secció transversal i $\mathbf{q = u \cdot B}$ és el transport (cabal) a través de l'àrea de la secció transversal.
Ara tenim només una equació ambd dues incògnites, l'elevació $\mathbf{\zeta} (x)$ i el transport $\mathbf{q}(x)$. Per resoldre-la necessitem una equació més que es pot obtenir amb l'ajut de l'equació de continuïtat. Per a un oceà de densitat constant tenim que,
\[ \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} = 0 \]
Si ara considerem que no hi han variacions en la direcció (y) i integrem verticalment multiplicant per l'amplada de la badia arribem a:
$$\bbox[10px, border:2px solid red] { \dfrac{\partial q}{\partial x} + B \;\dfrac{\partial \zeta}{\partial t} = 0, \quad (6) }$$
(5) i (6) són llavors les dues equacions a resoldre.
El model es basa en les equacions del moviment lineritzades, integrades verticalment afegint l'equació de continuïtat en la forma derivada en la pàgina anterior:
$$\bbox[10px,border:2px solid red] {\begin{eqnarray} \dfrac{\partial q}{\partial t} + g S \dfrac{\partial \zeta}{\partial x} & = & 0 \\ & & \\ \dfrac{\partial q}{\partial x} + B \dfrac{\partial \zeta}{\partial t} & = & 0 \label{eqn} \end{eqnarray}}$$
Una marea co-oscil·latòria és una marea estacionària generada per moviment mareal a l'extrem obert de la badia o golf. Podem suposar que le solucións per $\zeta (x, t)$ i $q(x, t)$ es poden factoritzar com
\begin{eqnarray*} \zeta (x, t) & = Z(x) \; e^{i \omega t} \\ q (x, t) & = Q(x) \; e^{i \omega t} \end{eqnarray*}
on $\boldsymbol{\omega}$ és la freqüència de la component mareal i $i$ denota el complex $i = \sqrt{-1}$. Introduïnt aquestes formes funcionales en les equacions trobem un conjunt d'equacions acoblades per $\mathbf{Z}(x)$ i $\mathbf{Q}(x)$:
\begin{eqnarray*} i \omega \; Q + g\; S \; \dfrac{d Z}{d x} & = 0 \\ \dfrac{d Q}{d x} + i \omega \;B\; Z & = 0 \end{eqnarray*}
Aquestes equacions es poden resoldre numèricaments si l'amplada $\mathbf{B}$ i l'àrea de la secció transversal $\mathbf{S}$ varien lentament en $x$. Podem dividir el domini d'x al llarg del golf o badia en trams de longitud $\mathbf{\Delta x}$ i fer els càlculs en diferències finites:
\begin{eqnarray*} Z_{k+2} & = & Z_k - \dfrac{2 \;i \;\omega \;\Delta x}{g \;S_{k+1}} \;Q_{k+1} \\ Q_{k+1} & = & Q_{k-1} - 2\; i\; \omega\; B \;\Delta x \;Z_k \end{eqnarray*}
El càlcul comença en la capçalera del golf amb $Q_0 = 0$ and $Z_1 = 1$, on $Q$ i $Z$ es calculan en seccions alternes.
L'efecte de la fricció del fons sobre l'ona de marea pot incorporar-se a través d'un terme lineal de decaïment. Si la fricció s'assumeix que és perpendicular a la velocitat del fons, que és proporcional al transport $\mathbf{q}$, les equacions verticalment integrades esdevenen
\begin{eqnarray*} \dfrac{\partial q}{\partial t} + g\; S \;\dfrac{\partial \zeta}{\partial x} + r \;q = & 0 \\ \dfrac{\partial q}{\partial x} + B\; \dfrac{\partial \zeta}{\partial t} = & 0 \end{eqnarray*}
on $\mathbf{r}$ és el paràmetre de fricció; $1/\mathbf{r}$ correspond al temps sobre el qual l'amplitud mareal hauria decaigut un factor $1/e$ del seu valor original si el forçament mareal s'hagués aturat. Les equacions en diferències finites són llavors
\begin{eqnarray*} Q_{k+1} & = & Q_{k-1} - 2\; i\; \omega\; B\; \Delta x\; Z_k \\ Z_{k+2} & = & Z_k - \dfrac{2 \;(i \omega + r) \;\Delta x}{g \;S_{k+1}} \;Q_{k+1} \end{eqnarray*}
El Golf de Spencer és un dels dos golfs que s'estenen cap al nord des del vessant sud d'Austràlia (Figura 1, veure més detalls a Easton, 1978). Les marees al llarg de la costa sud d'Austràlia són moderades, amb unes amplituds de les 4 components més importants en el rang 0.15 - 0.30 m. Les marees en aquests golfs són generalment més fortes i augmenten cap a les capçaleres. La taula següent llista les constants de marea pels ports al voltant del Golf de Spencer i altres posicions.
| port | M2 | S2 | K1 | O1 |  |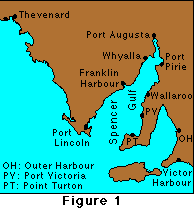
||||
| H (m) | fase (º) | H (m) | fase (º) | H (m) | fase (º) | H (m) | fase (º) | ||
| Golf de Spencer | |||||||||
| Port Agosta | 0.68 | 212 | 0.74 | 273 | 0.45 | 82 | 0.29 | 54 | |
| Port Pirie | 0.49 | 200 | 0.54 | 263 | 0.41 | 80 | 0.28 | 52 | |
| Whyalla | 0.42 | 185 | 0.45 | 245 | 0.40 | 73 | 0.26 | 45 | |
| Wallaroo | 0.17 | 130 | 0.17 | 187 | 0.32 | 62 | 0.22 | 34 | |
| Franklin Harbour | 0.22 | 114 | 0.23 | 173 | 0.30 | 61 | 0.20 | 24 | |
| Port Victoria | 0.18 | 70 | 0.18 | 127 | 0.23 | 52 | 0.20 | 24 | |
| Point Turton | 0.18 | 67 | 0.21 | 117 | 0.26 | 53 | 0.17 | 22 | |
| Port Lincoln | 0.23 | 35 | 0.26 | 87 | 0.23 | 29 | 0.16 | 2 | |
| Altres ports | |||||||||
| Outer Harbour | 0.50 | 105 | 0.49 | 176 | 0.25 | 50 | 0.16 | 24 | |
| Thevenard | 0.30 | 1 | 0.37 | 47 | 0.19 | 24 | 0.13 | 359 | |
| Victor Harbour | 0.14 | 343 | 0.14 | 46 | 0.18 | 30 | 0.14 | 356 | |
La taula mostra que les amplituds de les components M2 i S2 tenen un mínim al centre del golf prop de Wallaroo i que les fases d'aquestes camvien uns 180º des de la boca del golf a Port Lincoln fins la capçalera a Port Agosta; En altres paraules, aquestes dues components co-oscil·len amb les marees de l'oceà del sud com una seca de segon ordre. En contrast, les amplituds de les components K1 i O1 augmenten monotònicament desde la boca fins a la capçalera, i les seves fases són quasi constants al llarg del golf, indicant que aquestes components formen una seca de primer ordre.
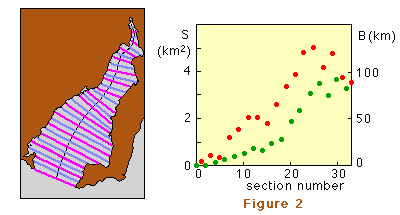La figura 2 mostra la divisió del golf en 33 compartiments de 10 km de llargada (Δ x del model de diferències finites) i l'associada amplada B (punts vermells) i àrea de la secció transversal S (punts verds). Els valors per B han de ser proveit per les possicions imparelles (línies magenta), els valors per S per les posicions parelles (línies en gris fosc).
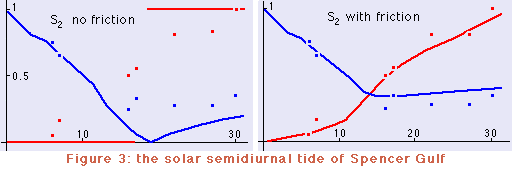
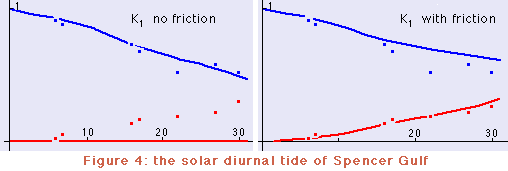
La figura 3 compara el resultat del model per a la component S2 amb les amplituds i fases observades. L'amplitud, normalitzada a la unitat a la capçalera del golf, es mostra en blau; la fase, normalitzada a (ie dividida per) 180º, es mostra en vermell. les observacions es mostren amb quadrats. (Notar que sense fricció la fase només pot ser igual a 0º o 180º.) La figura 4 dona la mateixa comparació per a la component K1.
La versió original d'aquesta eina estava dividida en dues parts: una per a mostrar només els càclculs numerics i una segona per a dibuixar els resultats. En aquesta versió s'ha remodelat tota la secció i ara es mostren els càlculs i es grafiquen conjuntament.
Es quantifica un factor d'amplificació que indica quan proper estem de la resonància de la badia i/o golf. Aquest factor es defineix com el quocient de l'amplitud a la capçalera dividit per l'amplitud a la boca. Cal recordar que l'amplitud a la capçalera està normalitzada a 1 i que els càlculs procedeixen de la capçalera cap a la boca, de forma que la ressonància no dona amplituds molt grans però produeix un factor d'amplificació molt gran.
Pel cas del golf de Spencer es calculen els errors quadràtics mitjos (rms) (un per a l'amplitud i un altre per a la fase) de cadascuna de les components (S2 o K1) on hi han observacions. Es compara el model amb els valors observats en els punts de mesura dels mareògrafs.
|
|
|
Dades badia Component: marea resultats |
Amplificació: Errors (rms): amplitud fase |