Ondas são deformações periódicas em uma interface. Em oceanografia, ondas de superfície são deformações da superfície dos oceanos, i.e., na interface oceano-atmosfera. As deformações se propagam com a velocidade de onda, enquanto as partículas descrevem movimentos oscilatórios ou orbitais com velocidade de partículas e permanecem, em mèdia, na mesma posição.

Em águas profundas, os caminhos das partículas são circulares. Em águas mais rasas, os caminhos percorridos pelas partículas se achatam e ficam parecendo elipses (Figura 9.1). Uma onda de águas profundas passa a ser considerada como de águas rasas quando o comprimento de onda $\lambda$ se torna maior do que o dobro da profundidade local da água $h$. As mudanças nas propriedades das ondas entretanto ocorrem antes disso, quando $\lambda = 20 h$. Portanto, é bastante útil se distinguir entre

  |_______________________________|________________________________|________________________
  0            < λ <             2h              < λ <            20h          < λ

      ondas de água profunda            ondas de transição            ondas de água rasa 
       ou ondas curtas                    ou ondas longas

Aqui é muito importante que notemos a distinção entre as ondas de águas profundas ou rasas tem quase ou nada a ver com a profundidade absoluta da água em um local, mas é determinada pela razão entre a profundidade local e o comprimento de onda. Os oceanos profundos podem ser considerados rasos em relação a ondas, desde que o comprimento de onda da mesma seja maior que o dobro da profundidade local. Esse é o caso das marés por exemplo.

Classificação das Ondas

As ondas nos oceanos podem ser classificadas de diversas formas. Uma classificação usa as forças que geram as ondas. Em ordem crescente de comprimentos de onda formados, nós temos:

1. Forças Meteorológicas (ventos e pressão atmosférica); aqui temos as ondas comuns em praia e o swell
2. Terremotos; eles geram os tsunamis, que são ondas de água rasa ou de ondas longas.
3. Marés (Forças gravitacionais dos astros); elas são sempre ondas de água rasa ou longas.

Outra classificação é baseada na representação do espectro de freqüência para todas as ondas oceânicas e distingue entre ondas capilares, ondas de gravidade, ondas de longo período, marés e ondas "transtidais" (Figura 9.2). Ainda uma outra classificação é baseada nas chamadas forças restauradoras, que são aquelas que trazem as partículas de água para a sua posição original na coluna de água (Figura 9.2).

Descrição das Ondas

A maneira mais simples de encarar as ondas é pelo conceito da onda como uma oscilação harmônica (Figura 9.3). Assim, podemos descrevê-las por

• seu período, $ \tau $
• sua freqüência, $ f = 1 / \tau$
• sua freqüência angular, $\omega = 2 \pi / \tau$
• seu comprimento de onda, $ \lambda $
• sua velocidade, $ c = \lambda / \tau $
• sua altura, $ H = 2\; A$ ($A$ = amplitude)
• sua inclinação, $\delta = H / \lambda $

A superposição de duas ondas com freqüências bem próximas $\omega_1$ e $\omega_2$ respectivamente, produz grupos de ondas ou séries (Figura 9.4). As cristas individuais propagam com uma velocidade de fase (idêntica a velocidade da onda) $c$; séries de ondas propagam com uma velocidade de grupo

\[ c_g = c - \lambda \; dc/d\lambda \]

(Nota para os mais fluentes em matemática: uma expressão mais convencional muito usada em oceanografia é $c_g = d\omega /d k$, onde $k<$ é o número da onda).

Apesar das partículas das ondas permanecerem na mesma posição em média, as ondas transportam energia em pacotes. A energia se propaga na mesma velocidade que a séries; ela pode se mover mais rápido ou mais devagar que cristas individuais. Isso se chama dispersão.

Dispersão Normal

Na dispersão normal, c aumenta com $c_g < c$, i.e. as cristas das ondas mais longas viajam mais rápido do que as cristas das ondas mais curtas. Como conseqüência, $c_g < c$, i.e. a energia viaja mais lentamente que as cristas das ondas. Isso ocorre nas ondas de gravidade como o swell.

Ondas não dispersivas

Aqui, $c_g = c$,, i.e., todas as cristas viajam com a mesma velocidade, e a energia também se propaga com a mesma velocidade.

Dispersão Anômala

Isso acontece quando $c_g < c$. As ondas capilares são um exemplo. A energia se propaga mais rápida que as cristas das ondas, e as ondas curtas viajam mais rápido que as ondas longas.

Na maior parte das condições oceânicas, a inclinação da onda é muito pequena e a velocidade da onda é portanto dada por

\[ c = \sqrt{\dfrac{g \lambda}{ 2 \pi} tanh \big(\dfrac{2 \pi h}{ \lambda}\big)},\quad \quad (\text{vàlida per a}\;\;\delta \lt \lt 1, \text{o}\; \lambda \gt \gt H)\]

Aqui, H é a altura da onda e h é a profundidade local. A fórmula pode ser simplificada ainda mais dependendo da razão de λ versus h:

Velocidade de ondas de água profunda (ondas curtas; a profundidade local é maior de 1/2 comprimento de onda)	\[ c = \sqrt{\dfrac{g \lambda}{ 2 \pi}} \]	$c_g = c / 2$ (dispersão normal)
Velocidade de ondas de água rasa (ondas longas; a profundidade local é menor que 1/20 do comprimento de onda)	\[ c = \sqrt{ g h} \]	$c_g = c$ (ondas não dispersivas)

Como um exemplo, considere ondas produzidas por uma tempestade distante. Na porção profunda em oceano aberto, essas ondas viajam como ondas de água profunda; sua velocidade de propagação de onda portanto depende se seu comprimento de onda λ. Assim, as ondas longas viajam mais rapidamente e chegam a maiores distâncias antes. Elas são sentidas como ondulação (ou "swell"). Quando a ondulaçãol se aproxima da costa, a profundidade local diminui e chega um ponto em que as ondas mudam para ondas de águas rasas. Como conseqüência, a velocidade da onda c diminui conforme a profundidade diminui e as ondas se inclinam para dentro; a frente da onda se torna progressivamente mais paralela a linha de costa

Ondas de amplitude finita

O conceito de oscilação harmônica nos dá uma boa descrição das ondas com inclinações bem pequenas. Ao se aproximar da costa, ou durante o período de formação ativa pelo vento, a inclinação da onda não é pequena o suficiente e o perfil da onda se desvia de um perfil harmônico. Conforme a inclinação aumenta, o perfil da onda se torna mais agudo:

Eventualmente, as ondas quebram. Os valores limites antes das ondas se quebrarem são 120º para o ângulo da crista e uma inclinação de δ = 1/8$\Delta = 1/8$. Ondas mais inclinadas não possuem um caminho fechado para as partículas em movimento orbital e estão associadas a um transporte de água (não apenas de energia). Esse transporte é chamado de deriva de Stokes, em homenagem a esse pesquisador.

Ondas curtas (ondas de água profunda)

Ondas curtas nos oceanos são ondas geradas pelo vento. Elas são divididas em dois grupos: vagas e ondulação (em inglês "sea" e "swell"). A vagas incluem todas as ondas formadas pelos ventos locais, enquanto a ondulação se refere a ondas geradas em campos de ventos distantes.

O efeito do vento no estado do mar depende da distância na qual o vento pode soprar sem obstáculos até o ponto que está sendo observado. Essa distância é conhecida como pista (em inglês "fetch"). A presença da costa limita a pista para ventos que sopram em direção ao oceano. Em mar aberto a pista é geralmente definida pelo tamanho do sistema de tempo (ou instabilidade) que produz o vento.

Outro fato determinante das ondas é o tempo no qual o vento sopra sem interrupção em uma data força. Para uma dada velocidade de vento, leva um certo tempo para que as ondas se formem e cresçam até chegar a um estado de equilíbrio dinâmico. O tempo para se chegar nessa equilíbrio (a partir do qual as ondas são incapazes de crescer) é conhecida como duração do vento.

Em qualquer instante de tempo, o estado do mar nunca apresenta uma oscilação harmônica única, mas aparece a um observador como um processo caótico. Assim, maneiras alternativas de descrever as condições de ondas foram encontradas, baseadas em quantidades estatísticas mensuráveis. Dois procedimentos são usados:

1. A determinação de parâmetros de onda significativos (descrições no domínio do tempo)
2. Determinação do espectro da onda (descrição no domínio da freqüência).

A coleção de muitos resultados resultou em estimativas de parâmetros de onda para os mares totalmente desenvolvidos (Figura 9.5). Um mar totalmente desenvolvido é aquele que tanto a pista quanto a duração do vento não são mais fatores limitantes (i.e., não ocorre mais crescimento), já que as perdas de momento e energia através das ondas quebrando estão em balanço com as entradas pelo vento.

O gráfico mostrado na Figura 9.5 se aplica a situações onde as ondas são geradas por ventos locais. A Figura 9.6 mostra propriedades de ondas para situações onde as mesmas foram formadas remotamente. Ela assume mares totalmente desenvolvidos na região de formação.

Para muitas aplicações marinhas, por exemplo, rotas de navios ou desenhos de plataformas, é necessário prever apenas as ondas mais altas. A quantia altura significativa da onda foi assim, introduzida. Essa é definida como a média do 1/3 ou 1/10 da ondas mais altas para um período de observação. ( O uso de $H_{1/3}$ é mais comum que o uso de $H_{1/10}$). De observações, as ondas mais altas possíveis $H_{max}$ se relaciona as alturas significativas de onda por

\[ \dfrac{H_{max}}{H_{1/3}} = 1.45 \quad \quad \text{é} \quad \quad \dfrac{H_{max}}{H_{1/10}} = 1.3 \]

As medidas de altura máxima de ondas dependem de certa forma do período de de tempo de observação; valores diferentes para _max são encontrados em séries de tempo de 10 minutos ou séries de 3 horas.

Descrição Estatística das Ondas

As relações entre as maiores ondas e as alturas significativas indicam que o estado do mar possui certas propriedades estatísticas. Uma descrição estatística é baseada na representatividade do campo do ondas através de um espectro de energia. Para uma dada freqüência, a energia da onda é proporcional ao quadrado da amplitude.

Um espectro de energia mostra a energia da onda em função de sua freqüência. Uma onda harmônica simples possui um espectro monocromático.

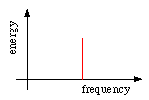
A descrição estatística assume que ondas em todas as freqüências e correspondentes comprimentos de onda estão presentes. Ela não tenta descrever a forma da superfície do oceano mas se concentra na energia das ondas. Num mar onde os ventos são fortes e com uma distribuição aleatória de energia de onda em todas as freqüências, a forma teórica do espectro de energia seria aquela de uma "curva normal" ou de distribuição Gaussiana. Aonde apenas a ondulação (swell) é presente, a energia se concentra próxima a freqüência da ondulação e o espectro é bem mais estreito:

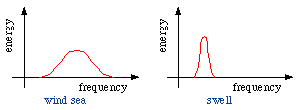
Em condições oceânicas normais, a energia não é aleatoriamente distribuída mas tende a decair rápido (em forma de cascata) das ondas com os menores comprimentos de onda possíveis misturadas pelo vento até as os comprimentos de onda maiores. Como resultado, o formato do espectro de ondas oceânico depende fortemente da velocidade do vento. A Figura 9.7 mostra espectros de energia observados para mares totalmente desenvolvidos em várias velocidades de ventos. Note que o espectro tende a ter uma distribuição normal apenas durante ventos fracos; conforme a velocidade aumenta, as ondas de menor período estão ainda presentes, mas a maior parte da energia é encontrada em ondas de maior período. O espectro então decai rapidamente em períodos maiores; ele é "desviado" em direção aos períodos mais longos.

O decaimento final da onda acontece quando a mesma quebra na praia, o que ocorre quando a velocidade da partícula se torna maior do que a velocidade de fase (onda individual). Nesse estágio, as ondas transportam energia e massa para a praia. Enquanto muita da energia é dissipada no retrabalhamento físico das praias, a massa de água que chega tem que retornar ao mar. Isso ocorre em intervalos regulares ao longo da praia nas chamadas correntes de retorno, um movimento forte de água em direção ao mar junto ao fundo ("vala").